Binary Search
Question 9: Given a sorted (in ascending order) integer array nums of n elements and a target value, write a function to search target in nums. If target exists, then return its index, otherwise return -1.
Normally, when we want to search for an element, the absolute worst case scenario is walking through each element until we find the target element. When the array is sorted, however, we can take advantage of this information and bring down the search time by a huge factor.
This is a nice gif explaining the power of binary search:
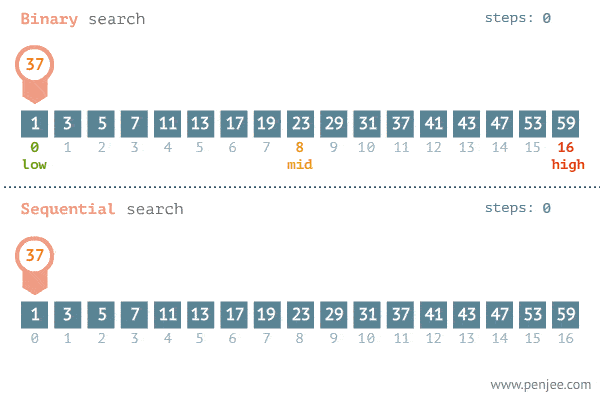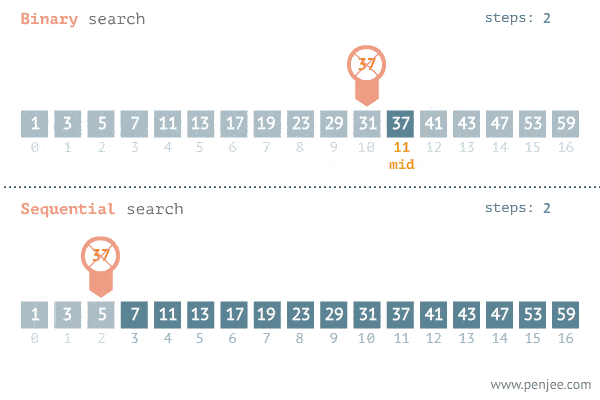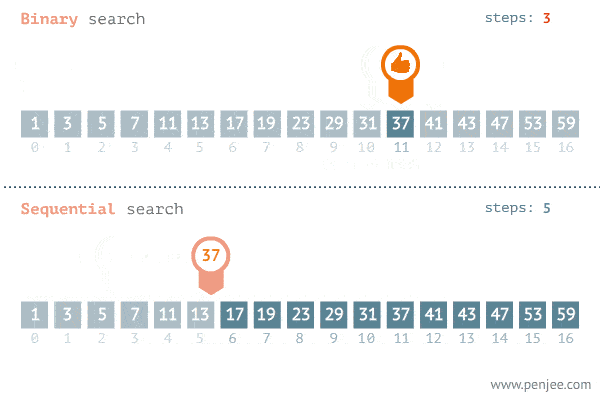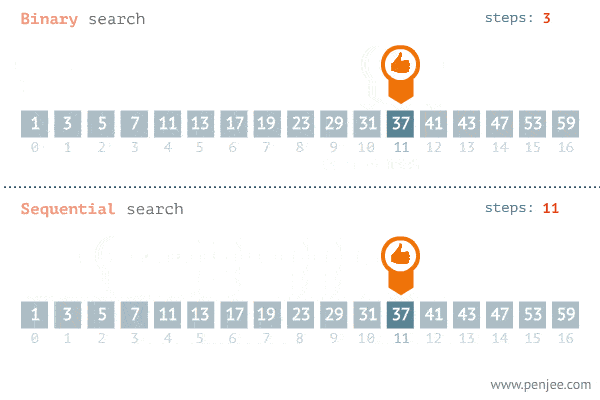
We are able to cut the number of nodes we look at by half at every iteration, and this is what brings about the large performance improvement. We build on the idea that the array is sorted, which allows us to know off-the-bat that values to the right of the value are greater, and values to the left are lesser.
Below is the code that implements binary search:
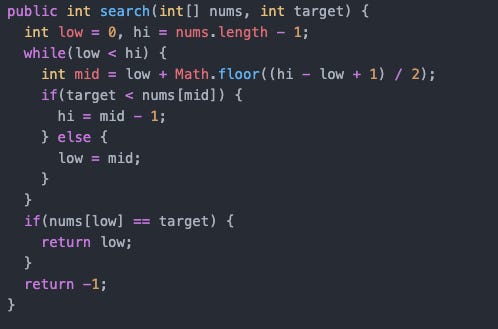
We define the variables low and hi. These two indexes work as boundaries such that we will only look at the elements in between these two.
Define mid variable. The mid variable defines the middle element in the boundary. It divides the nodes we look at into two parts. Mid helps us continually divide our array into two pieces at every iteration.
Compare target to mid. Through this comparison, we can determine which side of the mid variable to focus on. If the target is greater than mid, we can infer that the target must be on the right of target, since values to the right are greater. Vice versa if the target is less than mid.
Keep looping. The while loop only stops when low and hi are the same, which means we only have one element to look at. Assuming the target is in the array, we know that we have arrived at our target number.
We’re done!


