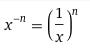Power of X to the N
Lessons learned: recursion
Due to the holidays, this will be the last SWEPrep post in 2020 . The good news is that we’ll be up and running in 2021. Thank you all for subscribing! 😁
Question: Given two integers x and n, write a function to compute x to the power of n. We may assume that x and n are small, and overflow does not occur. Type of x is a double, and n is an integer.
A different way of defining x to the power of n is simply saying it is equal to x to the power of two, to the power of n / 2, from the Identities of Exponents:
Since n is an integer, dividing by two will only be accurate for even numbers. For odd numbers it will be off by 1 (example: 3/2 == 1 if 3 is an int). So we add a check in the case that it is odd, we multiply the remainder back. In this case that would just be multiplying the result by another x.
We can solve this recursively, with base cases for n being 0 (return 1).
If n is negative (x to the power of -3 for example), we can simply flip the value of n (making it positive) and moving x to the denominator as per the Identity of Exponents:
The below code illustrates the above approach:
We’re done!