Question 6: Write a program to sort a stack such that the smallest items are on top. You can use an additional temporary stack, but you may not copy the elements into any other data structure (such as an array). The stack supports the following operations: push, pop, peek, and isEmpty.
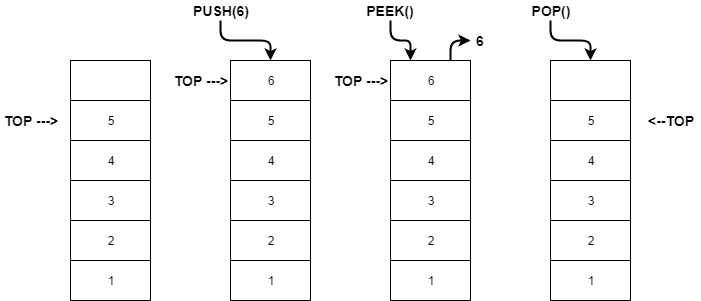
Before going into the solution, here’s a nice diagram I found explaining different stack operations (more information here):
A quick, brute force solution to sort would be merely find the minimum element in the stack and remove the element into a new stack, and perform this function over and over again. This would actually involve an additional, third stack. We need s1 for the given stack, s2 to collect/return the sorted stack, and s3 to take the values you pop from s1 as you find the minimum element.
Instead of finding the minimum element at every iteration, we can do something a bit more efficient. Let’s say that s1 is our given stack, and s2 is an already sorted stack. How would we bring the top value of s1 into s2, and ensure s2 is sorted? Let’s pop s1’s top value as a temporary variable. Then we can pop s2’s values into s1 so long as they are less than the temporary variable. Once this is done, we push the temp variable to s2. If we continue to perform the above steps again and again, soon all of s1’s values will be sorted into s2.
The below diagram explains the above steps visually:
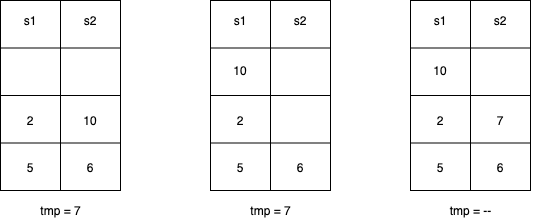
In the above step s2 pop’s its top element (10) into s1 since it’s greater than the tmp variable (7). Since 6 is less than 7, we can push tmp to s2 and preserve sorting.
As you can see we left the element 10 in s1, which is fine. Despite s2 pushing values back to s1, we can still reach efficient sorting and complete these steps for all of s1’s values. When 10 is the tmp variable, it will always just go right on top of s2 (it's in s1 precisely because it’s larger than the current top value of s2). In other words, we don’t lose efficiency because there won’t be any work to pop s2’s elements in the case where tmp is 10.
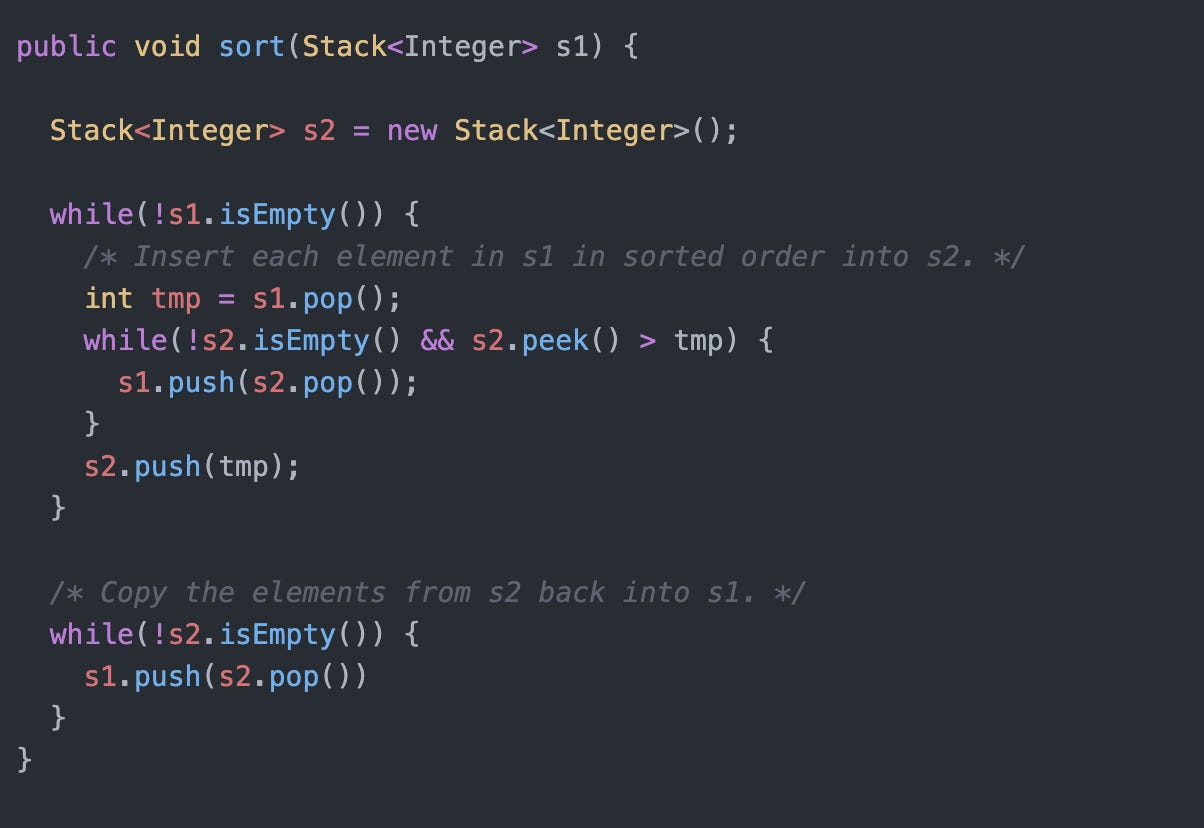
Below is the code for this solution:
We’re done!


